Perceptron

A Perspective and Feedback Loop of Insights

There is something called a Perceptron. It is a simple input output unit modeled off of a biological neuron instantiated via mathematics fulfilled programmatically.

You remember your Linear Algebra, Calculus, Statistics and Probabilities right? Of course you do!…

Well, I don’t

Yet, I wanted to learn enough about how “AI” works so I could build a particular project idea. I thought it would be cool to learn how to use machine vision to collect wildlife statistics off a stationary camera.

This is proving to be a difficult challenge, so in my quest to understand and better utilize the underlying structures. I pursued the knowledge that helps me to implement the ideas more effectively at a smaller scale to succeed at my project goal.

This was supposed to be simple when I started writing… As usual. it’s a rabbit hole.

Projects Teach Best

When I was in college I built a solar + battery power system to power my dads pond pump with all the solar I could collect from the cheapest panels I could find to charge a battery. I only had enough resources to obtain a system to supply 1/3rd of the power necessary. My goal was to break even in cost within seven years.

This means the total cost of the project would have to be less than the cost of the grid electricity which it replaces over that 7 years. 8 Cents/kWhr at ~0.2kW consumption for 8/12months and 0.1kW for 4/12 months.

That’s around ~500$ in electricity and turns out to be nearly impossible, nor does it account for my personal labor. However, the lessons learned have provided valuable insight which aided my jump into a career as an automation controls engineer.

While my grander ambitions of having the Pond camera locally track the pond wildlife as a source of data. Which can be later be visualized and facilitate an AI feedback loop for collecting useful data from stationary IP cameras. Getting the software implemented locally is a challenge requiring a lot of python code, labeling, and data management.

I discovered an online tool called roboflow, which has everything needed. Upload the data, label the data, train a model, use that to help you label more images, fix the mistakes as you go, train again to make the model better, repeat this feedback loop until you’ve got a near self sustaining improvement loop. Unfortunately, I was only able to train twice before my free credits were used. I have a GPU so I went looking for opensource software, I landed on ultralytics for it’s simplicity of use. I exported the labeled data from roboflow but I had labeled it in the wrong format, so I can either go back and relabel the 500 images without the help of the fancy online tools, or I could find another way. After trying to use code to modify the labels to match the needed format for many days I decided I needed to learn more about why my labels were not working.

This lead me deep down the layers of abstraction to:

The Perceptron

The perceptron while not related to the image detection algorithms solves a specific challenge related to my solar battery. Specifically the ability to determine if the battery is supplying power to the pond or the grid. We should be able to determine this using the Amperage and Voltage signals which I am collecting from sensors on the Battery power cables. The battery is between 24-30V at any given point during a 24hr period. The average ranges between 0-20A depending during the same cycle.

While you’d be correct that we don’t necessarily need a method like the perceptron to determine the state of this system, it provides a model simple enough you could potentially work the math out on paper while providing a programmable framework which requires the minimum amount of human input to obtain super high quality results which improve over time.

This provides a great opportunistic window for visualizing some important concepts which underpin AI learning.

The Perceptron

A perceptron is one early type of artificial neuron used in machine learning, which forms the foundation of neural networks. It is a simple model of a biological neuron in a mammalian brain. Let's break down how it works both mathematically and programmatically:

Mathematically:

1. Inputs and Weights:

   • Consider inputs

     \(x_1, x_2, ..., x_n\)

     where each input corresponds to a feature of the data.

   • Each input

     \(xi\)

     ​is associated with a weight

     \(wi\)

     Weights are parameters that the perceptron learns during the training process.

2. Linear Combination:

   • The perceptron computes a weighted sum of its inputs:

     \(\sum_{i=1}^{n} w_i \cdot x_i \\)

     often written as

     \(w⋅x\)

     in vector form.

3. Addition of Bias:

   • A bias term

     \(b\)

     (also a learnable parameter) is added to the weighted sum to shift the decision boundary away from the origin and is not dependent on any input value.

4. Activation Function:

   • The weighted sum plus bias is then passed through an activation function. The most basic form is a step function:

     \( f(z) = \begin{cases} 1 & \text{if } z \geq \text{threshold} \\ 0 & \text{otherwise} \end{cases} \)

   • Here,

     \(z = w \cdot x + b\)

5. Output:

   • The output is either 1 or 0, representing two classes for a classification task.

Programmatically:

Here's a simple implementation in Python:

import numpy as np

class Perceptron:
    def __init__(self, num_inputs, threshold=100, learning_rate=0.01):
        self.weights = np.zeros(num_inputs + 1)  # +1 for bias
        self.threshold = threshold
        self.learning_rate = learning_rate

    def predict(self, inputs):
        summation = np.dot(inputs, self.weights[1:]) + self.weights[0]
        return 1 if summation > 0 else 0

    def train(self, training_inputs, labels):
        for _ in range(self.threshold):
            for inputs, label in zip(training_inputs, labels):
                prediction = self.predict(inputs)
                self.weights[1:] += self.learning_rate * (label - prediction) * inputs
                self.weights[0] += self.learning_rate * (label - prediction)

In this implementation:

• num_inputs is the number of features in the input data.

• threshold is the number of epochs or iterations over the training dataset.

• learning_rate determines the size of the steps taken during the optimization process.

• train method updates the weights based on the prediction errors.

Training Process:

1. Initialize the weights and bias to zero (or small random values).

2. For each piece of data in the training set:

   • Compute the output.

   • Update the weights and bias if there is an error (the predicted output differs from the actual label).

The perceptron “learns” by adjusting the weights to predict the correct class labels of the input samples. It's a linear classifier and thus can only learn linear decision boundaries.

You might then ask: What does the input training data look like?

Let’s use the three attributes I have available:

Voltage, Amperage, Timestamp

I want the output to be True or False if the circuit is powered or not. The voltage range is 24-30V and the amperage is between 0-20A. Its measuring the power of the lithium battery. I want to train the “perceptron” with the fewest labeled data points as possible. I can provide data at the beginning of the day right as the solar powers up the battery sufficiently and at night when it runs below cutoff threshold.

Once we have a rudimentary model we can run against the live data(inference) we can continue collecting data whenever the prediction changes. From 1-0 or 0-1, this will allow us to continually optimize the output, only requiring human input for the first initial data.

We can Visualize the data like this:

Since the data is time based I though it might help to add arrows to illuminate the data’s sequence.

Next we train the perceptron on the data and plot the line.

Hmm this is frustrating, a single Perceptron creates a classical linear relationship and won’t fit the data correctly. Let’s add another layer.

The Multi-Layer Perceptron (MLP) model with one hidden layer has been trained on the normalized data, and the decision boundary is visualized above. it’s a little better than before but still doesn’t get all the points correct.

A few points to note:

• The MLP can create non-linear decision boundaries, as evident from the plot.

• The decision boundary appears to be more complex than the linear boundary created by the perceptron, which lead to better classification of the "on" and "off" states but still missed some.

• The warning about the optimizer not converging suggests that the training process might require more iterations or adjustments in hyperparameters (like learning rate) for optimal performance.

• Despite this, when I tried more learning, it did not improve.

Let’s try adding another hidden layer.

The MLP model, now with two hidden layers, has been trained and its decision boundary is visualized above.

This visualization demonstrates the capability of MLPs to handle more complex relationships in data compared to simple linear models like perceptron’s. All but one data point is accounted for.

• The addition of another hidden layer allows for even more complex decision boundary shapes.

• This can potentially improve the classification of data points, especially in scenarios where the relationship between variables is complex.

As with any neural network, it's important to monitor for signs of overfitting, where the model becomes too tailored to the training data and may not generalize well to new, unseen data. The choice of hyperparameters, such as the number of hidden layers and the number of neurons in each layer, should be based on the complexity of the data and the specific requirements of the task. Let’s add one additional layer.

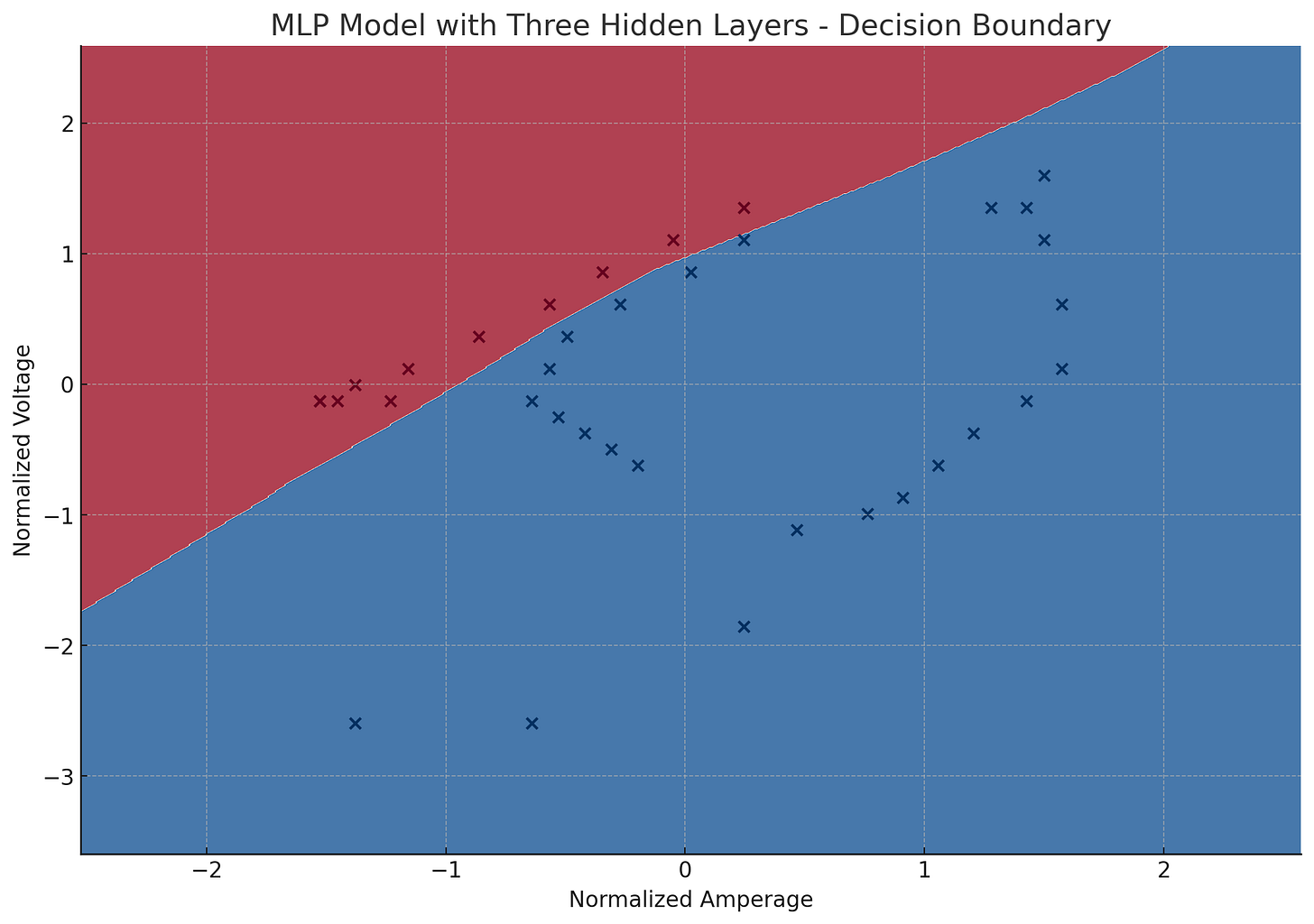
I trained the MLP model with three hidden layers, and its decision boundary is visualized above. We got all the data predicted points correctly!

• With three hidden layers, the model is now more complex, allowing for an even better fit to the data.

• However, with increasing complexity, there's also a higher risk of overfitting, especially if the dataset is not very large. We will need to collect the real world data to continue improving this model.

This visualization should give you an idea of how the additional complexity impacts the model's decision-making process. The decision boundary can become increasingly intricate with more hidden layers, which may or may not lead to better real-world performance, depending on the nature of the data and the task.

Training Data

Training a perceptron to ever more accurately estimate whether my pond inverter circuit is powered by the lithium battery based on Voltage and Amperage requires me to collect high quality data.

I want my data to reflect these key scenarios:

when the solar powers up the pond pump in the morning

and

when it switches back to grid after voltage cutoff threshold at night.

My training dataset should consist of examples with four attributes (Grid State, Voltage, Amperage, and Timestamp).

Structure of Training Data:

1. Attributes (Features):

   • Voltage (V): Numerical values ranging from 24V to 30V.

   • Amperage (A): Numerical values ranging from 0A to 20A.

   • Timestamp(ts): Unix Encoded timestamp

2. Label (Target):

   • Circuit Status: A binary label, such as 1 for "Powered" and 0 for "Not Powered".

Example Dataset:

dataset = [
    {"Voltage": 24, "Amperage": 10, "Circuit Status": 0},
    {"Voltage": 25, "Amperage": 5,  "Circuit Status": 0},
    {"Voltage": 27, "Amperage": 15, "Circuit Status": 1},
    {"Voltage": 30, "Amperage": 20, "Circuit Status": 1},
    {"Voltage": 29, "Amperage": 18, "Circuit Status": 1},
    {"Voltage": 24, "Amperage": 2,  "Circuit Status": 0},
    # ... made up data points ...
]

Data Collection Strategy:

• Morning Data (Solar Powering Up):

  • Collect data points right as the solar starts powering up the battery. Record the voltage and amperage readings along with a label indicating the circuit is "Powered" (1).

  • Example: If at the start of the day, the voltage is 27V and amperage is 15A, and the circuit is active, your data point would be [27, 15, 1].

• Night Data (Below Cutoff Threshold):

  • Collect data points at night when the battery runs below the cutoff threshold. Again, record the voltage and amperage readings with a label indicating the circuit is "Not Powered" (0).

  • Example: If at night, the voltage drops to 24V and amperage to 10A, and the circuit is inactive, the data point would be [24, 10, 0].

Moving from a basic perceptron to more advanced models has helped us in addressing the primary limitation of the single layer perceptron: its inability to model non-linear relationships. A perceptron, by its nature, is a linear classifier, which means it can only learn linear decision boundaries. This is sufficient for linearly separable problems, but our real-world data requires capturing more complex, non-linear patterns.

Non-Linear Models:

1. Multi-Layer Perceptrons (MLPs) / Feedforward Neural Networks:

   • MLPs consist of multiple layers of perceptrons, typically organized into an input layer, one or more hidden layers, and an output layer.

   • Each neuron in a hidden layer transforms the values from the previous layer with a weighted linear summation followed by a non-linear activation function, like ReLU (Rectified Linear Unit), Sigmoid, or Tanh.

   • This architecture allows MLPs to learn non-linear relationships.

2. Activation Functions:

   • In a basic perceptron, the activation function is usually a step function. In MLPs, non-linear activation functions enable the network to learn complex patterns.

   • ReLU: Common for hidden layers, especially in deep networks, because it helps alleviate the vanishing gradient problem.

   • Sigmoid or Tanh: Often used in output layers for binary classification (Sigmoid) or when the output needs to be normalized (Tanh).

3. Backpropagation and Gradient Descent:

   • In MLPs, training involves backpropagation, a method for calculating the gradient of the loss function with respect to each weight by the chain rule, efficiently propagating the error backward through the network.

   • Gradient descent (or its variants like Adam, RMSprop) is used to adjust the weights to minimize the loss.

Advantages of MLPs Over Basic Perceptrons:

• Ability to Capture Non-Linearity: This is the most significant advantage, allowing the model to solve problems that are not linearly separable.

• Flexibility and Customization: The architecture (number of layers and neurons) can be adjusted to suit the complexity of the task.

• Generalization: MLPs are better at generalizing from the training data and making predictions on unseen data, provided they are not overfitted.

Use Cases for MLPs:

• Complex Classification Tasks: Like image recognition, speech recognition, or advanced time-series analysis.

• Regression Problems: Where the relationship between input and output is non-linear.

• Feature Extraction: In deep learning, layers of an MLP can act as feature extractors, transforming the input data into a more useful representation for the task at hand.

After coming to the point where I realized a basic perceptron is insufficient due to the complexity of the data, I added layers, even then I found that to be insufficient.

What’s the next level?

After the Multi-Layer Perceptron (MLP), the "next level" in the evolution of neural network architectures involves more sophisticated and specialized types of networks. Each of these advanced architectures is designed to handle specific types of data and solve complex problems that MLPs might struggle with. Here are some key advancements:

1. Convolutional Neural Networks (CNNs):

   • Best For: Image processing, computer vision tasks.

   • Key Features: Use of convolutional layers that automatically and efficiently learn spatial hierarchies of features from input images. These are great for tasks like image classification, object detection, image segmentation, etc.

2. Recurrent Neural Networks (RNNs) and Long Short-Term Memory Networks (LSTMs):

   • Best For: Sequential data, like time series, speech, and text.

   • Key Features: Ability to process sequences of data, remember previous inputs in memory, and use this memory to influence the current output. LSTMs are an advanced version of RNNs, capable of learning long-term dependencies.

3. Transformers:

   • Best For: Natural Language Processing (NLP), but also increasingly used in other areas.

   • Key Features: Utilize self-attention mechanisms to weigh the importance of different parts of the input data. They have become the foundation for state-of-the-art models in NLP, like BERT and GPT.

4. Graph Neural Networks (GNNs):

   • Best For: Data that is best represented as a graph (e.g., social networks, molecular structures).

   • Key Features: Operate on graph structures, capturing the relationships and interconnections between data points effectively.

5. Generative Adversarial Networks (GANs):

   • Best For: Generating new data that's similar to the training data, especially in image generation.

   • Key Features: Consist of two networks, a generator and a discriminator, that are trained simultaneously in a game-theoretic approach.

6. Reinforcement Learning (RL) Models:

   • Best For: Decision-making tasks, like game playing, robotics, autonomous vehicles.

   • Key Features: Learn to make a sequence of decisions by interacting with an environment to achieve a goal.

Each of these architectures introduces new principles and mechanisms beyond the capabilities of MLPs. They are tailored to specific types of data and tasks, allowing for more efficient learning and better performance in complex scenarios. The choice of architecture depends heavily on the nature of the problem and the data you're working with.

Going any deeper into the specifics is beyond this article, but I wanted to leave you with the structured feedback loop which I used to collect my data.

While none of this directly translated to the greater wildlife data capture project. The feedback loop is similar.

First, human collects data, labels the data, and trains a model on the data.

Then we use the model to make predictions on the continuous stream of real data, find the outliers and false positives, have humans remove or fix their labels, and then retrain.

We repeat that gathering and training until we have a model of sufficient accuracy for our task.

This demonstrates two things: The human feedback loop is very helpful for learning inside the feedback loop of machine learning.

There are techniques for when human labeling is too cumbersome, which I am exploring now. Until next time…